Available Questions Page 1 of 1
Case-Based Questions
A shop selling electronic items sells smartphones of only three reputed companies A, B and C because chances of their manufacturing a defective smartphone are only 5%, 4% and 2% respectively. In his inventory he has 25% smartphones from company A, 35% smartphones from company B and 40% smartphones from company C.
(i) Find the probability that it was defective.
(ii) What is the probability that this defective smartphone was manufactured by company B ?
Sol:
Three students, Neha, Rani and Sam go to a market to purchase stationery items. Neha buys 4 pens, 3 notepads and 2 erasers and pays ₹ 60. Rani buys 2 pens, 4 notepads and 6 erasers for ₹ 90. Sam pays ₹ 70 for 6 pens, 2 notepads and 3 erasers.
(ii) Find $|A|$ and confirm if it is possible to find $A^{-1}$.
(iii) (a) Find $A^{-1}$, if possible, and write the formula to find $X$.
OR
(iii) (b) Find $A^2 - 8I$, where $I$ is an identity matrix.
Sol:
Based upon the results of regular medical check-ups in a hospital, it was found that out of 1000 people, 700 were very healthy, 200 maintained average health and 100 had a poor health record.
Let $A_1$: People with good health,
$A_2$: People with average health,
and $A_3$: People with poor health.
During a pandemic, the data expressed that the chances of people contracting the disease from category $A_1$, $A_2$ and $A_3$ are 25%, 35% and 50%, respectively.
(ii) Given that the person has not contracted the disease, what is the probability that the person is from category $A_2$ ?
Sol:
Camphor is a waxy, colourless solid with strong aroma that evaporates through the process of sublimation, if left in the open at room temperature.
A cylindrical camphor tablet whose height is equal to its radius (r) evaporates when exposed to air such that that the rate of reduction of its volume is proportional to its total surface area. Thus, $\frac{dV}{dt} = kS$ is the differential equation, where V is the volume, S is the surface area and t is the time in hours.
(ii) Substituting $V = \pi r^3$ and $S = 2\pi r^2$, we get the differential equation $\frac{dr}{dt} = \frac{2}{3}k$. Solve it, given that $r(0) = 5$ mm.
(iii) (a) If it is given that $r = 3$ mm when $t = 1$ hour, find the value of k. Hence, find t for $r = 0$ mm.
OR
(iii) (b) If it is given that $r = 1$ mm when $t = 1$ hour, find the value of k. Hence, find t for $r = 0$ mm.
Sol:
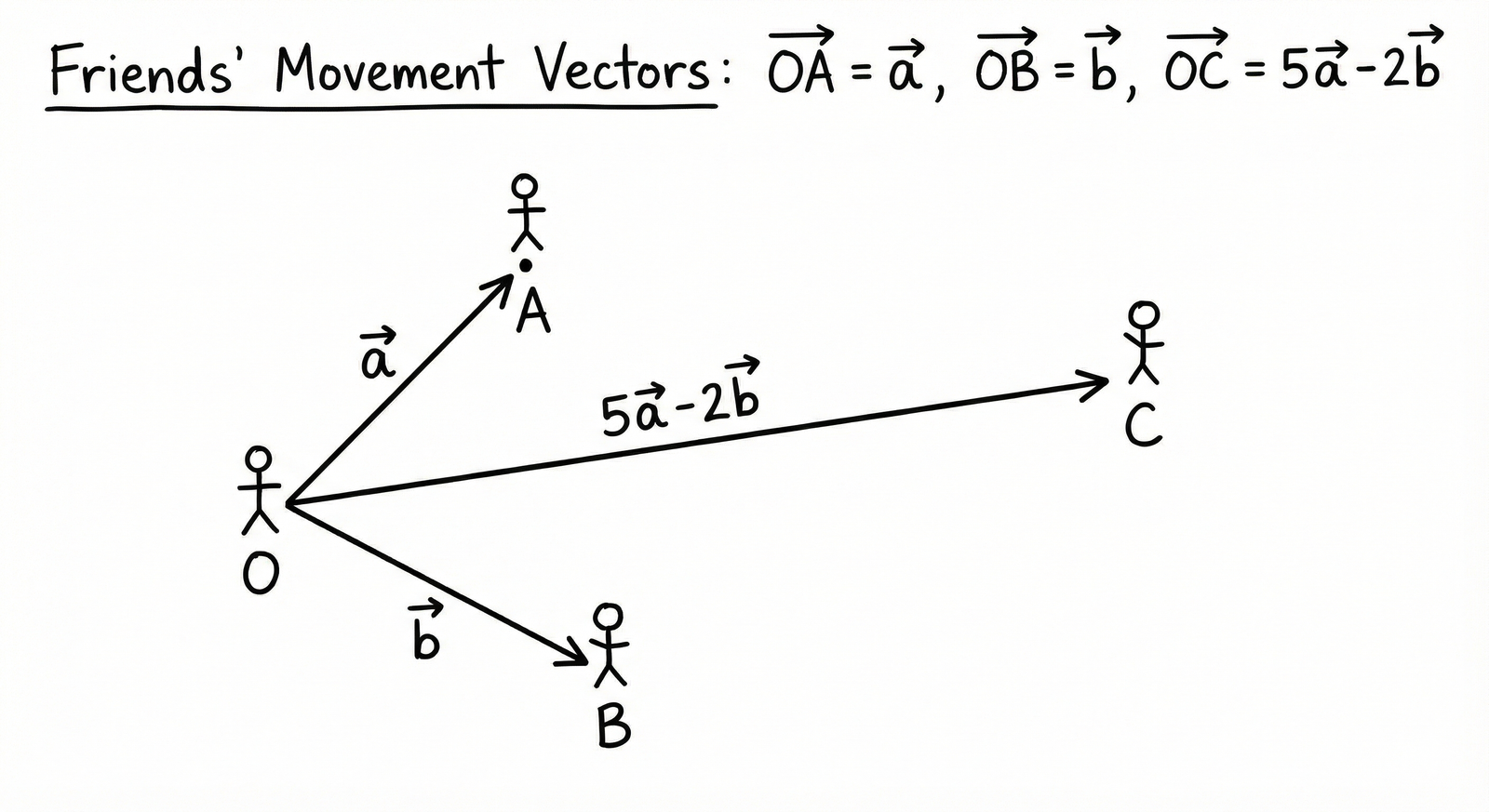
Three friends A, B and C move out from the same location O at the same time in three different directions to reach their destinations. They move out on straight paths and decide that A and B after reaching their destinations will meet up with C at his predecided destination, following straight paths from A to C and B to C in such a way that $\overrightarrow{OA} = \vec{a}$, $\overrightarrow{OB} = \vec{b}$ and $\overrightarrow{OC} = 5\vec{a}-2\vec{b}$ respectively.
(ii) Find vectors $\vec{AC}$ and $\vec{BC}$.
(iii) (a) If $\vec{a} \cdot \vec{b} = 1$, distance of O to A is 1 km and that from O to B is 2 km, then find the angle between $\overrightarrow{OA}$ and $\overrightarrow{OB}$. Also, find $|
\vec{a} \times \vec{b}|$.
OR
(iii) (b) If $\vec{a} = 2\hat{i} - \hat{j} + 4\hat{k}$ and $\vec{b} = \hat{j} - \hat{k}$, then find a unit vector perpendicular to $(\vec{a}+\vec{b})$ and $(\vec{a}-\vec{b})$.
Sol:
A technical company is designing a rectangular solar panel installation on a roof using 300 metres of boundary material. The design includes a partition running parallel to one of the sides dividing the area (roof) into two sections.
Let the length of the side perpendicular to the partition be $x$ metres and with parallel to the partition be $y$ metres.,
x and y..
Sol:
Sol:
Sol:
Sol:

A bank offers loan to its customers on different types of interest namely, fixed rate, floating rate and variable rate. From the past data with the bank, it is known that a customer avails loan on fixed rate, floating rate or variable rate with probabilities 10%, 20% and 70% respectively. A customer after availing loan can pay the loan or default on loan repayment. The bank data suggests that the probability that a person defaults on loan after availing it at fixed rate, floating rate and variable rate is 5%, 3% and 1% respectively.
Sol:
Sol: